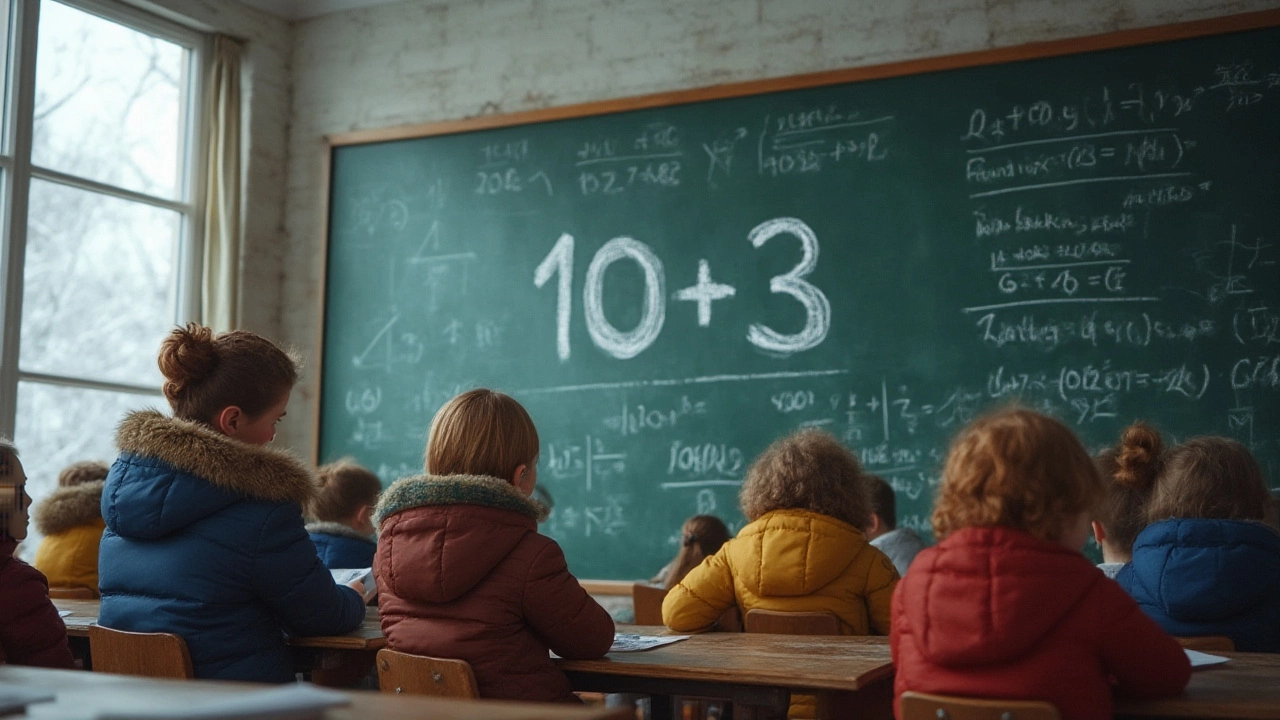Попробуй представить себе число 1000. Просто, да? А теперь запиши его как 10^3. Вот тут уже начинаются вопросы: зачем эти экспоненты, почему не написать просто 1000, и почему так часто эта запись встречается в статистике, спорте, науке и даже на шоколадках? Причём даже кот Барсик смотрит на калькулятор, будто это какое-то особое заклинание. На самом деле коэффициент 10^3 — штука, которую ты видишь чаще, чем думаешь, даже если не осознаёшь этого. Числа растут быстро, жизни не хватает считать нолики, а тут бац — простая надпись экономит кучу времени.
Что такое коэффициент 10^3 простыми словами
Если отбросить всю заумь, 10^3 — это способ сказать «1000» всего тремя символами. Число 10 — это база, а цифра 3 вверху показывает, сколько раз число 10 нужно умножить само на себя. То есть:
- 10 × 10 = 100
- 100 × 10 = 1000
Хотя кажется, что этим пользуются только в лабораториях, ты удивишься, где встречается 10^3 в обычной жизни. На килограммах, где приставка «кило-» и есть те самые 10^3 грамм. Дистанции — километр, килобайт, киловатт. Даже где-то на беговой дорожке может светиться 1 Км, и означать тысячу метров, хотя многие путают километры с милями. Разница между 1 000 и 10^3 только в том, что последнюю запись проще читать, особенно если речь о чем-то вроде 10^8 — цифры перестают прыгать перед глазами, и гораздо легче сравнивать значения между собой.
Я лично встречал в букмекерских конторах — когда речь шла о количестве ставок, или о разнице в коэффициентах выигрыша. Если кто-то указывает результат в тысячах, проще обойтись 10^3 и не париться с лишними ноликами, которые путают даже продвинутых пользователей сайтов.
Где и зачем используют коэффициент 10^3?
Разумеется, такой способ записи не просто для украшения. Когда цифр становится очень много, а места на экране или бумаге совсем мало — экспоненты спасают ситуацию. Вот несколько любопытных областей:
- Научные расчёты. Астрономы постоянно пользуются 10^3 и круче — расстояния до звёзд, массы, объёмы вещества. Зачем писать 1 000 000, если можно 10^6?
- Информатика и техника. Килобайт — это 10^3 байт. Хочешь узнать, сколько мегабайт в терабайте? Записывай экспоненты, складывай показатели — и не ошибёшься в порядке.
- Спорт и статистика. Тут коэффициент 10^3 встречается в статистике посещаемости, выручки, средней дистанции в марафоне и даже при анализе ставок на матчи. Представь, что у тебя есть посещаемость стадиона в 40 тысяч человек и 55 тысяч — написать 4 × 10^4 и 5.5 × 10^4 куда нагляднее для сравнения.
- Ежедневные штуки — пакеты на 1000 грамм называются килограмм. Пакеты с киловольтами, килолюменами — всё это 10^3 чего бы то ни было.
Когда видишь где-то запись 10^3 — не страшно, а спасительно: читаешь быстро, не теряешься в нулях, а понимаешь масштаб сразу. Даже кот Барсик знал бы, что 10^3 вкусняшек — это ровно три пачки по 333 штуки с плюсом.

Чем удобна экспоненциальная запись в ставках и спорте?
Обычно, когда слышишь слово "коэффициент" в ставках, думаешь о шансах на победу — типа 1.8 или 2.45. Но сама экспоненциальная запись — это ещё и приём повышения прозрачности в той же спортивной статистике или аналитике ставок. Вот целая таблица для разбора, почему это действительно удобно:
| Обычное число | Экспоненциальная запись | Удобство |
|---|---|---|
| 1 000 | 10^3 | Просто визуально покороче |
| 10 000 | 10^4 | Нулей меньше, ошибок в подсчёте меньше |
| 100 000 | 10^5 | Проще сравнивать с меньшими/большими числами |
| 1 000 000 | 10^6 | Всё читается мгновенно при анализе |
Особенно весело сопоставлять ставки по странам. Например, в Англии и Германии общий объём ставок на футбол часто превышает 10^9 евро в год — миллиард, но вместо 1 000 000 000 выглядит аккуратно и сразу видно разницу. В турнирах наподобие Лиги чемпионов тоже привыкли показывать доходы и расходы клубов с помощью экспоненциальной записи. А когда ты разбираешь маржу букмекеров, вот тут экспоненты ценные, ведь автоматизация всех расчётов требует понятных форматов данных. Чем меньше ошибок в интерпретации, тем меньше риск попасть «в минус» на длинной дистанции.
Журналистам и футбольным аналитикам тоже милее короткая экспоненциальная запись: её быстрее печатать, легче считывать, удобнее вставлять в графики или сводные таблицы.
Согласись, такой подход нужен не только для экономии места, а чтобы просто не «ловить глюков» из-за лишнего нолика.
Как читать и использовать коэффициент 10^3 в повседневной жизни и на ставках
Самый простой лайфхак: если видишь 10^3, сразу преобразуй это в тысячу. Если встречаешь 10^6 — миллион. Не трать время на подсчёт ноликов, просто помни:
- 10^3 — тысяча
- 10^4 — десять тысяч
- 10^5 — сто тысяч
- 10^6 — миллион
В ставках иногда пишут «сумма выигрыша: 2 × 10^3 рублей» — вот, пожалуйста, две тысячи никак иначе. И когда видишь подобную запись в приложении или на сайте, уже не бросаешься проверять — не ошибся ли автор с количеством нулей.
В спортивной статистике часто считают среднюю посещаемость, или сумму голов, или бюджет в 10^8 — считай, это сто миллионов. Практично, удобно, и графики радуют глаз.
Есть ещё совет: если ты учишься пользоваться калькулятором, обзаведись научным калькулятором — там экспоненты вводятся одним нажатием, а риск ошибиться минимален. Даже вписывая коэффициенты вручную, проще держать в голове правило — степень всегда показывает, сколько нулей должно быть у десятки.
Барсик, кстати, оценит и другой лайфхак. Если пишешь быстро, поставь «k» вместо 10^3 — во многих чатах и на форумах так и делают: "у меня 2к подписчиков", вот тебе и две тысячи. Главное не путай с такими же «к» для температуры — в науке это уже кельвины.
Если есть дети, не забудь эту тему объяснить им на примерах из жизни: килограмм яблок на рынке, десятитысячные гран-при Формулы-1, топовые бюджеты футбольных клубов, просмотры видео на YouTube. Это позволяет смотреть на мир другими глазами — осознаёшь масштаб и не зависаешь на пересчётах.